SEQUÊNCIA DIDÁTICA - BRINCANDO COM TANGRAM

SEQUÊNCIA DIDÁTICA – BRINCANDO COM TANGRAM

OBJETIVOS:

• Identificar as formas: triângulo retângulo, quadrado, paralelogramo em distintas posições e algumas de suas propriedades;
• Trabalhar implicitamente com ângulos;
• Identificar a semelhança de figuras planas; 
• Estimular a produção textual;
• Promover a construção de figuras geométricas.

TURMA: 5ª e 6ª série

TEMPO ESTIMADO:

Duas aulas

DESENVOLVIMENTO Atividade 1: Construção do Tangran de 7 peças usando folhas brancas A4 e tesoura

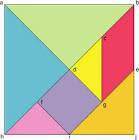
Trabalhar com a geometria plana através de um milenar quebra-cabeça chinês, também conhecido como As Sete Tábuas da Astúcia, formado por sete figuras geométricas: 5 triângulos, 1 quadrado e 1 paralelogramo, obtidos da decomposição de um quadrado maior como mostra a figura abaixo:

Antes de iniciar as atividades geométricas e montagens de figuras, equivalência e medidas de perímetro contar aos alunos duas das várias lendas que cercam esse misterioso quebra-cabeça.

Observação: Ao final de cada passo, o aluno deverá responder algumas perguntas em seu caderno. Aproveite a construção para rever com os alunos alguns conceitos geométricos como: diagonais de um polígono, tipos de quadriláteros, tipos de triângulos, altura de um triângulo, semelhança de triângulos, etc.

1º. PASSO - Peça aos alunos que construam e recortem o maior quadrado possível a partir de uma folha A4.

Pergunta 1: O quadrado que você construiu é um retângulo? É um paralelogramo? É um losango? É um trapézio? Justifique suas respostas.

2º. PASSO – Desenhe uma das diagonais do quadrado e utilizando uma tesoura, recorte o quadrado pela diagonal. Que tipo de figura geométrica é cada uma das peças obtidas após o corte?

 
Pergunta 2: Classifique as figuras de acordo com os lados e com os ângulos. Justifique.

3º. PASSO – Guarde um dos triângulos formados no passo anterior. No outro, vamos marcar a altura em relação à hipotenusa. Como fazer? Basta dobrar o triângulo a partir do ângulo reto. Após isto, recorte ao longo desta dobra (a altura), formando dois triângulos. (Estes dois triângulos que surgiram após o corte são as duas primeiras peças do tangran).

Pergunta 3: Estes dois triângulos menores são semelhantes ao triângulo maior que ficou reservado? Justifique.

4o. PASSO – Reserve esses dois triângulos menores. Vamos trabalhar agora com o triângulo maior que ficou guardado no 3º. PASSO. Utilizando este triângulo (triângulo maior) marque sua altura em relação ao ponto O à hipotenusa como no 3º. PASSO, mas não o recorte. Após esta dobra, você observará que marcou o ponto médio da hipotenusa do triângulo maior (o ponto médio do maior lado do triângulo grande). Agora, projete, ou melhor, leve o vértice do ângulo reto até esse ponto médio e dobre. Abra a figura e veja que há um novo triângulo, menor que os outros que estão reservados. Esta é a terceira peça do Tangran: o triângulo médio. Recorte esse triângulo e reserve.

Pergunta 4: Que tipo de quadrilátero é a figura que restou após recortar o triângulo? Justifique. 

5º. PASSO – Dobre o trapézio ao meio e recorte. Veja que apareceram duas figuras que também são trapézios. Reserve um deles. Com o outro trapézio você deverá formar um quadrado e um triângulo pequeno. Como?! Observe bem o trapézio, note que ele tem dois ângulos retos, um ângulo agudo e um obtuso. Dobre o trapézio fazendo coincidir o vértice do ângulo agudo com o vértice do ângulo reto adjacente. Abra. Você viu que apareceu um quadrado e um triângulo? Corte na linha e separe as figuras que são duas novas peças do Tangram, isto é, o quadrado e um triângulo pequeno. Já temos, portanto, 5 peças.  

Pergunta 5: Que tipo de trapézios são formados após dobrar e recortar o trapézio maior ao meio? Justifique.

6º. PASSO – Pegue o trapézio reservado no passo anterior. Dele sairão às duas últimas peças: um paralelogramo e um triângulo pequeno. Como?! Observe novamente o trapézio e agora faça coincidir o vértice do ângulo obtuso com o vértice do ângulo reto não adjacente a ele. Abra e observe a figura. Você verá um triângulo pequeno e a última peça do Tangram que é um paralelogramo (par de lados paralelos). Agora basta recortar as duas figuras. 

  AVALIAÇÃO

O professor deverá avaliar a participação dos alunos na construção das peças do Tangram. Através da participação durante cada passo, explicação e justificativa dada explicando o raciocínio. Observação do professor da compreensão apresentada.

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=266